タイムバンク市場分析【売買代金と市場規模の相関性①】

1 タイムバンク市場の「発行済時間総額」と「推定売買代金」の関係性を分析
2 数値の定義
3 分析
4 第１回まとめ

タイムバンク市場の「発行済時間総額」と「推定売買代金」の関係性を分析

今回は、本ブログで算出してきた「発行済時間総額」と「推定売買代金」のデータを利用して、二つのデータの関係性を調べます。

なぜこの分析を行おうと考えたかと言うと、これまでの「発行済時間総額」と「推定売買代金」のグラフに一定の関係性がありそうに見えたためです。

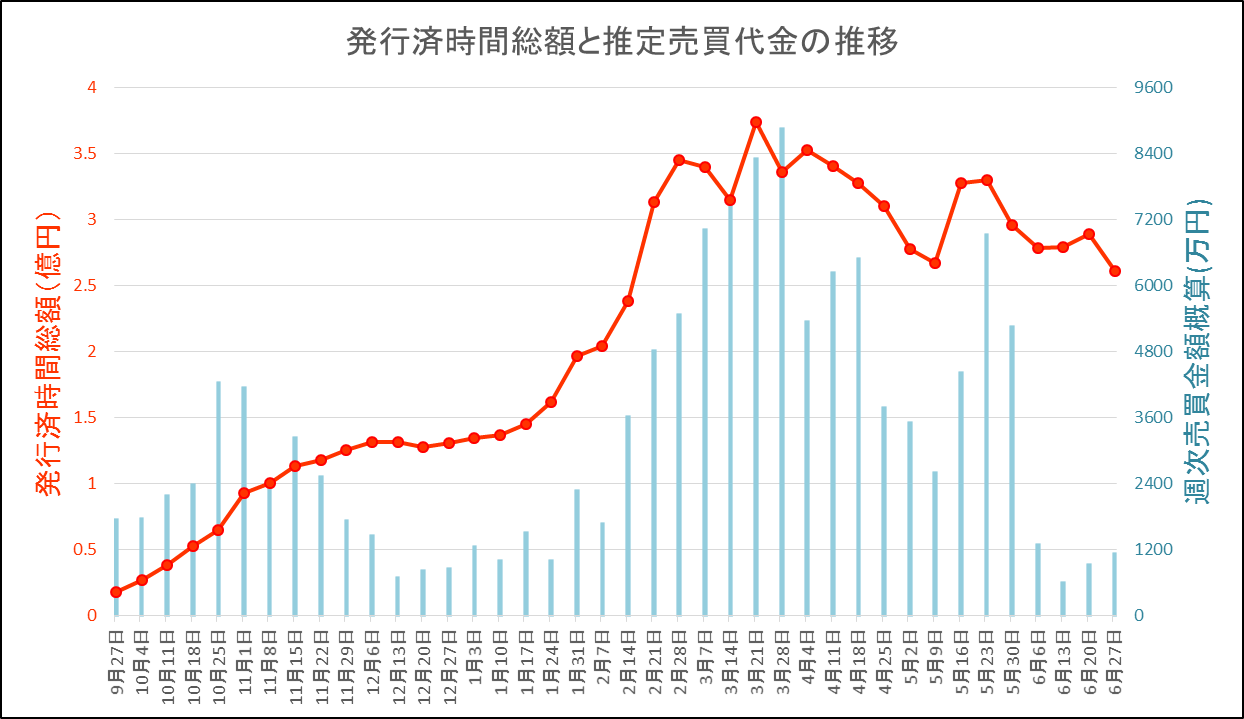
全体的に、推定売買代金(青)が増加しているタイミングで、発行済時間総額(赤)も増加しているように見えますよね。一方が増加すればもう一方も増加し、一方が減少すればもう一方も減少する。これは「正の相関がある」と言われ、式に落とし込むことで将来の予測を行う事も可能です。

「分析とか興味ない」という方でも、最終的に回帰式(予測式)を算出していますので、タイムバンクで取引をする上で役に立つのではと思います。

本テーマは２回に分けて執筆予定で、第１回は散布図からの相関係数と近似式の算出を行います。第２回は、第１回の結果を踏まえ、タイムバンク市場の実情を考察していきます。

それでは、次の項目から具体的な内容に入ります。

数値の定義

分析に利用してる二つのデータ、「発行済時間総額」と「推定売買代金」の算出方法です。

発行済時間総額：各銘柄の【発行時間×終値】の合計
推定売買代金　：各銘柄の【出来高×終値】の合計(１日毎に算出)

発行済時間総額は、タイムバンク市場の規模を、推定売買代金(※)はタイムバンク市場１日毎の取引高を表します。

※「推定」と付けているのは、売買代金の上記の計算方法は実態とは異なるためです。実態の値にするには、取引が発生する毎に【取引価格×取引秒数】を計算し、１日分の取引を合計する必要がありますが労力的に不可能です。そこで、「その日の取引はすべてその日の終値で取引された」と仮定して１日の売買代金を【出来高×終値】により推定しています。この計算方法は、一銘柄だけなら大きなばらつきが発生しますが、数百銘柄で数日に渡るデータとなれば、実態値に収束する確率が高いと考えています。

分析

分析手法は「単回帰式分析」

今回行うのは「単回帰式分析」。これは、一つの原因と一つの結果の関係性を明らかにする分析で、分析としては最も容易な手法の一つです。高校や大学でやった方も多いのではないでしょうか。例えば、喫茶店における「気温」と「アイスコーヒーの注文数」のように、原因である「気温」から、結果である「アイスコーヒーの注文数」を予測したりすることが可能です。

今回で言うと、原因が「推定売買代金」で、結果が「発行済時間総額(=市場規模)」です。市場規模が拡大するということは、各銘柄が値上がりする、という事ですので、関係性を明らかにすることで、売買のタイミングの目安とすることも可能だと考えています。

相関係数の算出

改めて、タイムバンクリリース(2017年9月後半)～2018年6月末までの「発行済時間総額」と「推定売買代金」の関係図を掲載します。

まず、タイムバンクリリース～6月末までの全期間での相関係数を求めます。この期間の「発行済時間総額」と「推定売買代金」の関係を散布図に表すと、次の表になります。

緑円で囲んだあたりが、タイムバンクリリース(2017年9月後半)～2017年12月前半までなのですが、これらが下に外れています。それ以外のデータはだいたい右肩上がりの線形になっている印象ですね。

とりあえず外れているデータも入れて計算した結果、相関係数は次の通りになりました。

相関係数(全期間)：0.64

0.64という相関係数は、一般的に”やや相関がある”と言われていますが、相関係数としてはイマイチですね。やはり緑円あたりのデータが外れているので、相関係数を下げてしまっています。

おそらく、タイムバンクリリース(2017年9月前半)～2018年12月前半までは、市場が初期段階で不安定であったと考えて良いでしょう。この時期は通常の発行時間が72000秒で、現在の通常の発行時間18000秒より多く発行されていたことも影響していると思われます。

したがって、緑円の中のデータは、現在の市場分析を行うのに用いるのは適切ではないと考え、今回は考慮しないことにします。

2017年12月13日～2018年6月末の相関係数の算出

上の図から緑円のデータを取り除いた散布図が次の図です。

だいぶ直線らしくなりました。2018年6月のデータがまとまって外れているのが気になりますが、この考察は第２回に譲ります。

これらのデータから相関係数を計算すると、以下の数値になります。

相関係数(2017年12月13日～2018年6月末)：0.79

相関係数は約0.8となり、”かなり強い相関がある”という結果が得られました。この結果なら、「推定売買代金と発行済時間総額には強い正の相関がある」と言えそうです。つまり、「推定売買代金が上昇すると、発行済時間総額が上昇し、すなわち各銘柄の価格が上昇する」という推測がある程度の根拠をもって成り立ちます。